Corriente
Alterna
Cuando
se descubrió la electricidad muchos de los avances originales de esta fueron desarrollados
en base a la corriente continua. Las primeras luminarias, las primeras máquinas,
las primeras centrales. Pero más adelante se empezó a emplear en la industria eléctrica
la corriente alterna debido a que es más fácil su transporte y distribución.
Corriente
Continúa
Se
caracteriza en que el flujo de corriente siempre va en el mismo sentido de positivo de la fuente al negativo de esta y
sin fluctuaciones en la intensidad de dicha corriente.
Corriente
Alterna
Se caracteriza
por un flujo de corriente variable con sentido de circulación alternado. Las
formas de variación de la corriente Alterna pueden ser de diferentes clase, es así que tenemos
señales triangulares, dientes de sierra, cuadrada pero la más utilizada y la
que desarrollaremos en el presente capitulo es la señal senoidal.
Señal
Senoidal
Tanto en la ecuación como en la gráfica inicial vemos algunas cualidades a destacar
Una onda senoidal alterna va a tener los siguientes elementos
Amplitud maxima (Amp max) Es el máximo valor pico que obtiene la onda senoidal
Angulo de fase
Es el
ángulo de desfasaje entre una onda y una senoidal sin ángulo de fase. En otras
palabras sirve para representar el corrimiento entre ondas. Se dice que una
onda está en fase con otra cuando ambas tienen el mismo ángulo de fase y en
contrafase cuando el ángulo difiere 180°
Velocidad angular o frecuencia angular. W
Está
asociada al tiempo en que una onda tarda en volver a encontrarse en el mismo
punto inicial de partida y repetir su forma de onda
Se la
puede calcular de distintas maneras
W=2π*f o W=2π÷T
Donde f es la frecuencia de la onda y T es el periodo
Periodo (T)
Es el
tiempo que tarda la onda en volver a repetirse se mide en segundos
Frecuencia (f)
Es la
cantidad de veces por segundo que se repite una onda
Amplitud pico a pico
Es la
diferencia entre la amplitud máxima y la amplitud mínima en ondas señoriales es
dos veces la amplitud pico
Valor medio de la onda
Es el promedio de la onda a lo largo de un ciclo y arroja la componente de continua de la onda si es que la tuviera pero ya veremos esto más adelante en otra unidad. En este caso para ondas señoriales el valor medio de la onda senoidal es cero ya que en promedio tengo la misma parte positiva que negativa.
Valor Eficaz de la onda
Es el promedio cuadrático de la onda senoidal a lo largo de un periodo (promedio de la onda sin contar los signos) y para el caso de ondas senoidal es eléctricas está asociado a la energía que puede entregar la señal eléctrica) para ondas senoidales es
Representación
de magnitudes con sub índices
En
electrónica se pueden representar estas magnitudes con letras por ejemplo
Estos
sub índices son muy utilizados para diferenciar e informar características de
señales y deben prestarse suma atención porque nos indican que tipo de
información tenemos de la señal
Resolución
de circuitos Con Corriente alterna (Fasores)
El cálculo
de circuitos con corriente utilizando ecuaciones senoidales es muy complejo y
en cierta medida innecesaria ya que como observamos hay ciertas magnitudes que
se mantienen constantes en la ecuación de la onda senoidal y que no cambian con
el tiempo. Ellas son
-Frecuencia
-Amplitud
-Fase
Con estas tres magnitudes nosotros podemos decir que sobre nuestro circuito se encuentra aplicada una onda seniodal de tal magnitud con un determinado ángulo de fase y de una frecuencia dada y nos olvidamos u obviamos el comportamiento de la misma en cada instante de tiempo.
A
Este concepto se lo conoce como Fasor
Fasor
Es
una representación vectorial de una onda de una dada frecuencia en función de
su amplitud y Angulo de fase.
Antes
que nada debemos saber que hay dos formas de representar a una onda en forma
fasorial una es usando su valor pico y otra es usando su valor eficaz. En este
curso utilizaremos siempre el valor eficaz de la onda para representarla en
forma fasorial.
Nota:
Algo importante a tener en cuenta es que el análisis de un circuito en función
de su respuesta fasorial solo puede ser aplicado si todas las ondas que se
aplican al circuito tienen la misma frecuencia. De no ser así el circuito debe
ser resuelto en función del principio de superposición ósea mediante el estudio
de las diferentes ondas aplicadas al circuito por separado
Ejemplo 1
Supongamos que le aplicamos a un circuito la siguiente onda senoidal y queremos saber su fasor
Acá podemos calcular Varias cosas Primero podemos ver que el valor pico de la onda es de 311 v y que el periodo de la onda es de 0.02seg además como la onda arranca de 0 podemos decir que tiene un Angulo de fase de 0
Calculemos
pues cual sería la frecuencia de esta onda
Podemos escribir la ecuación de la onda asociada a la gráfica sabiendo que
Y que
W=314
rad/seg
Ejemplo 2
Supongamos que a la onda anterior aplicada al circuito se le superpone otra onda según se muestra en la grafica
Ambas ondas tienen el mismo periodo a simple
visto por ende tienen la misma frecuencia y la amplitud pico y eficaz de las
ondas sigue siendo ósea Vef=220 V
Ahora como podemos observar la nueva onda
(roja) esta corrida con respecto a la otra, lo que suele denominarse como desfasada
Para poder calcular el desfasaje que tiene esta
onda debemos recordar que 360 º es un periodo completo y equivalen a 0.02 seg
ahora la diferencia de tiempo que existe entre ondas es 0.0025 seg por lo tanto
aplicando regla de tres simple obtenemos el desfasaje correspondiente a ese
tiempo
360 º
------ > 0.02 seg
X
----------- > 0.0025 seg
X=0.0025*360º/0.02=45º
Podemos dejar esto sentado como una formula
Ahora nos resta saber el signo de este
desfasaje como podemos apreciar la onda roja empieza antes que la onda azul
entonces el signo del Angulo de fase es positive y podemos decir que la onda roja esta adelantada con respecto
a la Azul.
Ahora podemos expresar a la onda en forma
fasorial como
V2=220∟45º
Y la ecuación de la onda en función del tiempo
seria
Ejemplo 3
Ahora
supongamos que a la onda del ejemplo uno le agregamos otra onda tal lo indica
la figura
Ambas ondas tienen el mismo periodo a simple
visto por ende tienen la misma frecuencia y la amplitud pico y eficaz de las
ondas sigue siendo ósea Vef=220
Como en el caso anterior podemos observar que
la nueva onda (roja) esta corrida con respecto a la otra, lo que suele
denominarse como desfasada. En
tiempo el corrimiento es de 0.005 seg entonces el Angulo de desfasaje es
Ahora nos resta saber el signo de este
desfasaje como podemos apreciar la onda roja empieza después que la onda azul
entonces el signo del Angulo de fase es negativo y podemos decir que la onda roja esta atrasada con
respecto a la Azul.
Ahora podemos expresar a la onda en forma
fasorial como
V3=
220∟-90º
Y la ecuación de la onda en función del tiempo
seria
Representación de los fasores en el plano cartesiano
Los fasores son vectores como tales se pueden
representar en el plano cartesiano como vectores se suele usar el modelo de
números complejos para encuadrarlos dentro de un concepto matemático así que en
el plano cartesiano que dibujaremos usaremos los ejes como Reales e
Imaginarios.
Al graficar estos vectores nos quedarían algo
así
Fasores y Números Complejos
De la misma manera que empleamos el plano
cartesiano que representa a los números complejos para representar los fasores,
podemos utilizar toda la matemática utilizada con números complejos para
calcular circuitos. Debido a esto he escrito un capitulo donde se explica el cálculo
con números complejos usado para corriente alterna el cual lo pueden encontrar
en este blog.
Ejemplo
Supongamos que queremos sumar los efectos
combinados de las tenciones de los ejercicios anteriores
Esto lo vamos a hacer de dos maneras analítica
(calculo) y gráficamente.
Forma analítica
V1=220∟0º
V2=220∟45º
V3=220∟-90º
VT=V1+V2+V3=220∟0º+220∟45º+220∟-90º
Como lo indica el anexo de Números Complejos y electrónica para realizar la suma de
magnitudes complejas todas deben estar en coordenadas rectangulares o binomicas
(parte real + parte imaginaria) por ende pasamos a rectangular todas las
magnitudes con la calculadora
Vt=220v+i0 +155.55+i155.55+0-i220
Ahora agrupamos las magnitudes reales por un
lado y las imaginarias por otro
Vt=(220v +155.55+0)+(i155.55-i220+i0)
Vt=375.5-i64.4
Y ahora si necesitamos podemos volver a pasar
la magnitud compleja a forma polar (modulo , Angulo)
VT=380.9∟-9.7º
Ahora en forma grafica
La forma gráfica que usaremos es a mi modo de
entender la más sencilla la cual
consiste en ir poniendo los vectores uno a continuación del otro y trazar la
resultante entre el punto de origen y el punto donde llega el ultimo vector
(cabe aclarar que a mí no me gustan los métodos gráficos )
Pues tenemos
Si se
hicieron las cosas bien (Cada uno de los vectores con la escala el valor y el Angulo
bien dibujados ) tenemos gráficamente una Vt igual a la Calculada
analíticamente . Lo cual se ve a simple vista en el grafico dibujado arriba .
Circuitos puramente resistivos y corriente alterna
Si conectamos una resistencia a una fuente de tensión
alterna , lo que obtendremos va a ser un flujo de corriente también alterno el
cual va a variar en fase con la
corriente que circula en la resistencia , ósea que a medida que la tensión en
la resistencia aumenta la corriente por la misma también aumenta en forma
proporcional de acuerdo a la ley de ohm
Tomemos el siguiente ejemplo
Si hacemos las cuentas
Ahora grafiquemos ambas ondas
Podemos ver que la tension y
la corriente estas en fase
Ahora que es lo que ocurre con
la potencia que se consume en la carga ya que tenemos dos ondas variantes en el
tiempo que se combinan en una resistencia , eso nos genera una potencia que
tambien es variante en el tiempo .
Recordemos que
Si graficamos la onda que nos
queda obtenemos
Aunque la corriente no se
alcanza a apreciar porque esta en una escala muy grande podemos decir que la
corriente y la tencion estan en fase . ademas podemos observar que la petencia
que consume el circuito es positiva lo que indica que toda la energia que se le
entrega a la resistencia es consumida por esta . pero esta grafica no nos da un
dato fundamental de la onda que es la potencia media
Potencia media
Es la potencia media consumida en un ciclo de
la onda en la resistencia y se obtiene de hacer un promedio integral de la onda
a lo largo de un ciclo de la misma. Osea según formula
Wow wow wow un segundo
cerebrito que cara jo es eso diran ustedes , no se asusten para este modulo
solo diremos que la resolucion de la ecuacion anterior es simple y que se
discutira en otra bollilla mas adelante
Pero como normalmente
trabajamos con valores eficaces
Que para el circuito anterior queda
Pmed=220v*22 A=4836 W
Circuito Puramente Capacitivo
Si conectamos un Capacitor a
una fuente de tension Alterna , obtendremos un circuito puramente capacitivo .
Recordemos que un capacitor es un elemento que almacena energia en forma de
campo electrico . Que es lo que ocurre cuando se lo conecta a una fuente de corriente alterna . bueno en la mitad del
semiciclo positivo el capacitor almacena energia , para luego debolverla en la
siguiente mitad del semiciclo .y asi sucesivamente. Esto proboca un defasaje
entre la tension y la corriente de 90 grados ya que cuando el capacitor empiesa
a almacenar energia la coriente es maxima y la tension es minima y cuando
empiesa a liberar energia la corriente es minima y la tension maxima es asi que
se dice que la corriente en un capacitor esta adelantada a la tension.
Ahora como tenemos una
corriente y una tension podemos suponer que tambien existe una relacion entre
ambas , a esta relacion se la conoce como reactancia capacitiva .
Donde la –j denota que la relacion
entre V e I estan desfasadas 90
Tomemos el siguiente ejemplo
basico
Xc =318 ∟-90 en cordenadas
polares
La tension como ya lo hemos
visto seria
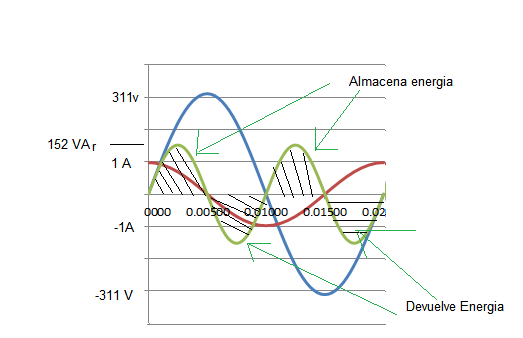
Si graficamos ambas curvas
obtenemos
Otro tema seria la potencia
veamos que susede si multiplicamos las dos curvas punto a punto y como se
analisa la potencia resultante
La cantidad de energia que el
capacitor almacena y luego devuelve es la misma por lo tanto el capacitor no
consume energia simplemente hace una transicion de energia la cual provoca una
circulacion de la misma atraves del circuito sin consumo alguno . A la potencia
asociada a esta energia se la denomina potencia
reactiva y su unidad no es el W (watt) sino el Var (Volt Amper Reactivo)
. y se calcula como
Q=-V*I=220
v * 0.691 A= 152Var
Circuito Puramente Inductivo
Si conectamos una bobina
a una fuente de tension Alterna ,
obtendremos un circuito puramente inductivo . Recordemos que una bobina es un elemento que almacena energia en forma de
campo magnetico . Que es lo que ocurre cuando se lo conecta a una fuente
de corriente alterna . bueno en la mitad
del semiciclo negativo la bobina almacena energia , para luego debolverla en la
siguiente mitad del semiciclo positivo .y asi sucesivamente. Esto proboca un
defasaje entre la tension y la corriente de 90 grados ya que cuando la bobina empiesa
a almacenar energia la tension es maxima y la corriente es minima y cuando
empiesa a liberar energia la tension es
minima y la corriente maxima es asi que se dice que la tension en una
bobina esta adelantada a la corriente.
Ahora como tenemos una
corriente y una tension podemos suponer que tambien existe una relacion entre
ambas , a esta relacion se la conoce como reactancia inductiva .
Donde la j denota que la
relacion entre V e I estan desfasadas 90
y L es la inductancia de la bobina
Tomemos el siguiente ejemplo
basico
Si graficamos ambas curvas
obteneomos
La cantidad de energia que la
bobina almacena y luego devuelve es la misma por lo tanto la bobina no consume energia simplemente hace una
transicion de energia la cual provoca una circulacion de la misma atraves del
circuito sin consumo alguno . A la potencia asociada a esta energia se la
denomina potencia reactiva y su unidad
no es el W (watt) sino el Var (Volt Amper Reactivo) . y se calcula como