Teorema de Thevenin
Introducción
Lo primero que piensa cualquier alumno cuando escucha este
nombre es “ya esta este seguro que lo desapruebo” pero no es la cosa mas
complicada del mundo.
Primero analicemos
para que sirve, el teorema de Thevenin se emplea para reducir circuitos
complejos en un circuito simple de una fuente una resistencia en serie y la carga,
aja y eso para que, bueno muchas veces sucede que en ciertos casos la carga que
se aplica a un circuito varia, eso provoca que halla que recalcular todo el circuito,
no obstante si el circuito fue reducido a un simple equivalente Thevenin esto
es mas fácil.
Otra de las razones es que muchas veces cuando analizamos un
circuito es mejor simplificar partes del mismo en un equivalente thevening.
En el sig esquema se ilustra
esto
Teorema de Thevenin
Enunciado
Una parte de un circuito lineal (*) ,comprendida entre los
terminales A y B puede ser sustituido por una fuente de Tensión
conocida como tensión
de thevenin Vth y una resistencia
Conocida como Resistencia de thevenin o Rth , actuando
estos elementos de manera análoga
a como se comportaría
el circuito original.
Bueno la teoría
en muy Bonita y la practica
como se lleva acabo
Para ello fiel a nuestro modus operandi desarrollaremos un
ejemplo y una serie de pasos a seguir, como ejemplo tomaremos el ya clásico y
famoso divisor resistivo, si no sabes que es un divisor resistivo ya lo veras
Ejemplo 1) Divisor resistivo con carga
Primero debemos hallar los dos componentes del circuito
equivalente, desarrollaremos por separado cada uno
Resistencia de Thevenin
1) Retiramos
la carga
2) Cortocircuitamos
las fuentes de tensión y borramos las fuentes de corriente
3) Mediante
método de serie y paralelo sacamos la resistencia equivalente que tengo entre
los terminales A y B
Paso 1 - Retiramos la carga
Pasó 2 –
Paso 3
Si observamos ambas resistencias tienen dos terminales en común
por ende están en paralelo y la R
resultante de este paralelo es la
Rth
Rth=10 ohm// 5 ohm =3,333 ohm
Tensión de Thevenin
1) Retiramos
la carga
2) Mediante
método de tensión entre dos puntos sacamos la tensión equivalente que tengo
entre los terminales A y B (nota al estar desconectada la carga la corriente
por esa rama se anula
Paso 1 - Retiramos la carga
Paso 2 – Mediante método de tensión entre dos puntos sacamos
la tensión equivalente que tengo entre los terminales A y B (nota al estar
desconectada la carga la corriente por esa rama se anula
Recordemos cuales son los pasos
de este método
1) Planteo las corrientes del circuito
2) Cálculo las corrientes del
circuito con algún método de resolución de circuitos (obviamente el que más me convenga)
3) Calculo la tensión entre los
puntos mediante la ley de Kirchhoff modificada
Prosigamos entonces
1- Planteo
las corrientes del circuito
2) Cálculo
las corrientes del circuito
Esto es fácil solo tenemos una malla así que vamos a
plantearla
12v=I * 5
OHM + I * 10 OHM
12V=I * (15
OHM)
12V/15OHM = I
3)
Calculo la tensión entre los puntos mediante la ley de Kirchhoff modificada
Voy a calcular la tensión VAB por
lo tanto Voy a ir desde A hasta B
Recordemos que
Dada
una trayectoria dentro de un circuito. La tensión de partida (VA) menos la
tensión de llegada (VB) mas la suma de las fuentes de tensión a lo largo de la
trayectoria tomada con su correspondiente signo es igual a la suma de todas las
caídas de tensión con su correspondiente signo que produzcan las corrientes el
circuito a lo largo de dicha trayectoria.
Va-Vb= I* 10ohm
Va-Vb=0.8 A* 10ohm=8V
Entonces VTH=8V
Ya tenemos los dos elementos correspondientes
al circuito equivalente thevening
Ahora solo nos queda expresarlos
Y listo ya podemos
calcular la respuesta al circuito ante diferentes valores de RC
Como este es un caso muy típico ,
desarrollaremos un ejemplo genérico
para cualquier divisor resistivo
Donde
Y
RTH se calcula como el paralelo
de R1 y R2
Ejemplo 2
Ahora si la
complicamos demasiado
Los
pasos son los mismos
Primero
calculemos la RTH
Resistencia
de Thevenin
1) Retiramos
la carga
2) Cortocircuitamos
las fuentes de tensión y borramos las fuentes de corriente
3) Mediante
método de serie y paralelo sacamos la resistencia equivalente que tengo entre
los terminales A y B
1)
Retiramos la carga
2)
Cortocircuitamos las fuentes de tensión
y borramos las fuentes de corriente
Ahora
por el método de reducción
por circuito equivalente sacamos la resistencia entre los terminales A y B
Quedando
el siguiente circuito equivalente
Como
ambas resistencias están en serie la Rtotal que en este caso es la Rth es de
Rth=7,49ohm
Paso
2 – Mediante método de tensión entre dos puntos
sacamos la tensión equivalente que
tengo entre los terminales A y B (nota al estar desconectada la carga la
corriente por esa rama se anula
Recordemos
cuales son los pasos de este método
1) Planteo las corrientes del circuito
2)
Cálculo las corrientes del circuito con algún método de resolución de circuitos
(obviamente el que más me
convenga)
3)
Calculo la tensión entre los puntos mediante la ley de Kirchhoff modificada
Prosigamos
entonces
1)
Planteo las
corrientes del circuito
2)
Cálculo las corrientes del circuito con algún método de resolución de circuitos
(obviamente el que más me
convenga)
Este
es un caso muy particular, observemos que
tengo dos mallas unidas por una sola rama R=5 ohm,
cuando esto ocurre lo que pasa es que no tengo circulación
de corriente entre ellas ósea I3 =0 A esto suelo
ocurrir cuando se realiza thevening y hay que estar atento,
y la corriente es cero porque no hay circuito
cerrado que permita su circulación, es como tener un
interruptor abierto en este caso el interruptor era la R de carga que retiramos del
circuito
Por
lo tanto solo tenemos que plantear dos mayas así que usaremos el
teorema de mayas
Malla 1
12 v – 3v =
I1 *15 ohm + I1 *1 ohm + I1 * 1 ohm
9 v=I1*(15
ohm + 1 ohm + 1 ohm )
9 v = I1
*(17 ohm)
9 v/ (17
ohm) = I1
0,529 A= I1
Malla 2
12 v + 5 v =
I2 * 7 ohm + I 2 * 2 ohm
17 v = I2 *
(7 ohm + 2 ohm)
17v = I2 *
9ohm
17 v / 9
ohm= I2
3)
Calculo la tensión entre los puntos mediante la ley de Kirchhoff modificada
Voy a calcular la tensión VAB por
lo tanto voy a ir desde A hasta B
Recordemos que
Dada
una trayectoria dentro de un circuito. La tensión de partida (VA) menos la
tensión de llegada (VB) mas la suma de las fuentes de tensión a lo largo de la
trayectoria tomada con su correspondiente signo es igual a la suma de todas las
caídas de tensión con su correspondiente signo que produzcan las corrientes el
circuito a lo largo de dicha trayectoria.
VAB+3V
– 5 V = - 7 ohm* I2 + 5v + I3 * 5 ohm –
I1* 1 ohm – 3v
VAB
= - 7 ohm* I2 + 5v + I3 * 5 ohm – I1* 1 ohm – 3v
VAB=-
7 ohm *(1.888 A )
+ 5v + 0A * 5 ohm – 0,529 A
* 1 ohm
VAB=-9,64 v+ 5v + 0v – 0,529 v
VAB=-5,16 v
Entonces VTH= -5,16 v
Por lo tanto el equivalente queda
Como Vth en negativo podemos
invertir la fuente de tensión
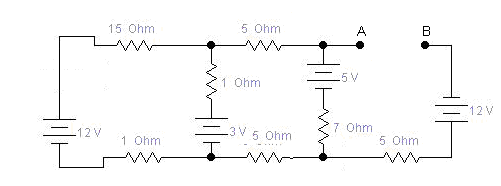
Ejemplo 3
Los
pasos son los mismos
Primero
calculemos la RTH
Resistencia
de Thevenin
1) Retiramos
la carga
2) Cortocircuitamos
las fuentes de tensión y borramos las fuentes de corriente
3) Mediante
método de serie y paralelo sacamos la resistencia equivalente que tengo entre
los terminales A y B
1)
Retiramos la carga
2)
Cortocircuitamos las fuentes de tensión
y borramos las fuentes de corriente
Ahora
por el método de reducción
por circuito equivalente sacamos la resistencia entre los terminales A y B
Quedando
el siguiente circuito equivalente
Paso
2 – Mediante método de tensión entre dos puntos
sacamos la tensión equivalente que
tengo entre los terminales A y B (nota al estar desconectada la carga la
corriente por esa rama se anula
Recordemos
cuales son los pasos de este método
1) Planteo las corrientes del circuito
2)
Cálculo las corrientes del circuito con algún método de resolución de circuitos
(obviamente el que más me
convenga)
3)
Calculo la tensión entre los puntos mediante la ley de Kirchhoff modificada
Prosigamos
entonces
1) Planteo
las corrientes del circuito
Como la rama de I5 esta abierta la corriente por esta rama
es igual a cero ósea I5=0
2)
Cálculo las corrientes del circuito con algún método de resolución de circuitos
(obviamente el que más me
convenga)
Volvemos a utilizar el método de las mallas por ser el más simple,
la rama de I5 no se plantea por que ya se sabe el resultado de dicha corriente
Malla 1
12v-3v=I1*(15Ohm+1Ohm+1Ohm)-I2*1
Ohm
9v=I1* 17
ohm – I2* 1 Ohm
Malla 2
3v -5v =
I2*(1 ohm + 5 ohm + 7 ohm + 5 ohm) – I1 * 1 ohm
-2v = I2
*18 ohm –I1 * 1 ohm
Reordeno
-2v =–I1 *
1 ohm+ I2 *18 ohm
Planteo el sistema de ecuaciones
9v=I1* 17 ohm – I2* 1 Ohm
-2v =–I1 *
1 ohm+ I2 *18 ohm
No lo vamos a resolver detalladamente simplemente exponemos
los resultados de esta resolución
I1 = 0,524
A
I2 = -0,0819
A
Comparando las corrientes de malla con las corrientes reales
del circuito planteadas originalmente
I1= Im1= 0,524 A
I2=Im2-Im1=-0,0819
A-0,524 A=-0,605 A
I3=Im2= -0,0819 A
I4=Im2=-0,0819 A
3)
Calculo la tensión entre los puntos mediante la ley de Kirchhoff modificada
Voy a calcular la tensión VAB por
lo tanto voy a ir desde A hasta B
Recordemos que
Dada una trayectoria dentro de un
circuito. La tensión de partida (VA) menos la tensión de llegada (VB) mas la
suma de las fuentes de tensión a lo largo de la trayectoria tomada con su
correspondiente signo es igual a la suma de todas las caídas de tensión con su
correspondiente signo que
produzcan las corrientes el circuito a lo largo de dicha trayectoria
Va-Vb
– 5 V – 12 V = I 4 * 7 ohm + I5 * 5 ohm
Va-Vb
= I 4 * 7 ohm + I5 * 5 ohm + 5 V + 12 V
Va-Vb
= 0,0819A * 7 ohm + 0 A
* 5 ohm + 5 V + 12 V
Va-Vb=17,573
V
Vth=17,573
V
Entonces VTH= 17,573 V
Por lo tanto el equivalente queda