Teorema de Mallas
En el presente capitulo se
desarrolla el concepto de los teoremas de mallas mediante dos ejemplos
desarrollados paso a paso.
Definiciones
Antes de empezar debemos aclara
algunos conceptos que nada tienen que ver con este curso pero que son básicos
para el mismo
Nodos
Punto donde se unen tres o más ramas de un circuito
Ramas
Trayectorias del circuito entre
nodos
Mayas
Toda trayectoria cerrada a lo
largo de un circuito por Ej.:
Teorema de mallas
Este teorema es la base desde
donde las cosas se empiezan a complicar, deriva de los teoremas de Kirchhoff,
siendo una simplificación de las ecuaciones que este mismo arroja. En este
teorema se plantean unas Pseudo corrientes que atraviesan toda la malla (con
pseudo quiero decir corrientes imaginarias)
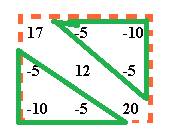
Veamos un circuito compuesto de
dos mayas para darnos una idea
Donde digo que tiene dos mallas
porque es el numero mínimo de mallas que necesito para que todas las ramas del
circuito queden incluidas dentro de al menos una malla.
Y como se resuelven las
corrientes con el método de las mallas, es simple aplicando el mismo
Teorema de Mallas
Dice algo así
La suma de las fuentes de tensión
a lo largo de una trayectoria cerrada con su correspondiente signo es igual a
la suma de todas las caídas de tensión con su correspondiente signo que produzcan las corrientes de mallas a lo
largo de dicha trayectoria.(Donde las corrientes de mallas son Pseudo
corrientes que circulan a lo largo de toda la malla)
Aja y eso que significa
Lo primero que hay que saber en
toda resolución de un circuito es que hay que ser metódico es decir seguir una
serie de pasos, conocidos para llegar al resultado deseado y correcto. (Siempre
que tengamos suerte y no metamos la pata en el medio)
En este caso definiremos 5 pasos
para resolver un circuito usando el método de las mallas que son
1-
Planteo de las corrientes reales del circuito
2-
Planteo de las corrientes de malla
3-
Obtención de las ecuaciones de mallas según las
corrientes de mallas antes planteadas
4-
Resolución de las ecuaciones de mallas
5-
Calculo de las corrientes reales del circuito
Como ejemplo didáctico (para que
en ves de chino sea ingles aunque sea) analizaremos el SIG circuito.
Paso 1: Planteo de las corrientes reales del circuito
Le asigno a cada Rama una
corriente con su respectivo nombre y sentido Ambos pueden ser cualquiera ya que
esto no afectara a la resolución hasta el Paso 5, a menudo lo que va a
ocurrir es que el profesor que nos de el ejercicio las asigne el.
De estas corrientes me conviene olvidarme
hasta resolver las ecuaciones de mallas
Pasó 2: Planteo de las corrientes de malla
Luego planteo las corrientes de malla:
siguiendo algunos tips que son
-
conviene que la corriente de malla tenga el mismo
nombre que una de la las corrientes de la rama que se esta planteando
-
el sentido de las corrientes de mallas influye en la
complejidad del las ecuaciones del circuito que estamos planteando , mas
adelante veremos que si planteamos las mayas en el mismo sentido de giro (es
decir todas con giro horario o todas con giro antihorario)obtendremos ciertas
ventajas practicas
Para el caso del circuito que estamos planteando usaremos
ambas mallas en sentido horario, luego explicaremos que ocurre en otros casos
con otros ejemplos
Quedando las mallas de la SIG forma
Pasó 3: Obtención de las ecuaciones de mallas
Este paso se divide en dos
facetas que explicaremos a parte en dos puntos y luego juntaremos para obtener
la ecuación de malla deseada, no se asusten por la extensión me e tomado la
molestia de explicarlo al detalle ya que si la ecuación de la malla se
encuentra mal planteada todo lo demás es Basura
Dada la ecuación general de la
malla enunciada anteriormente
Suma de fuentes de tensión en la
malla = suma de las caídas de tensión en la malla
Procederemos a usar este concepto
para desarrollar las ecuaciones de mallas según dos puntos que explican cada
una parte de la ecuación antes nombrada
Primer punto: Suma de las fuentes de tensión
La fuente de tensión que planteo
para cada malla tiene un signo asociado +/- , el planteo es simple, siguiendo
la malla si salgo por el terminal positivo la fuente es positiva, si salgo por
el negativo la fuente es negativa
Entonces para la malla uno me quedaría
la fuente de tensión 1 de 12V positiva porque salgo por el terminal positivo, y
la fuente de tensión 2 de 5v negativa porque salgo por el terminal negativo. Mientras
que para la malla 2 la fuente de tensión 3 de 12 V quedaría negativa porque
salgo por el terminal negativo, y la fuente de tensión 2 de 5v positiva porque
salgo por el terminal positivo tal lo
indica la Fig.
Entonces la parte de las
ecuaciones correspondientes a la malla uno quedarían así
Malla 1
V1 (Fuente 1)-V2 (Fuente 2)= suma
de las caídas de tensión en la malla 1
Ósea
12v-5v= suma de las caídas de tensión
en la malla 1
7v = suma de las caídas de tensión
en la malla 1
Como habrán notado cada vez que
me refiero a una fuente de tensión en las ecuaciones lo hago con la letra V
mayúscula
Malla 2
V2-V3= suma de las caídas de tensión
en la malla 2
5v-12v= suma de las caídas de tensión
en la malla 2
-7v= suma de las caídas de tensión
en la malla 2
Segundo punto: Suma de las caídas de tensión
El signo de las caídas de tensión
en la malla es positivo si la corriente que la produce va en el mismo sentido
que la corriente de la malla que estoy planteando y negativo en caso contrario.
Analicemos el circuito anterior
Partiendo de la fuente 1 y
siguiendo la malla 1 lo primero que me encuentro es la resistencia R1 de 10 ohm
la cual solamente es atravesada por la corriente de malla 1 teniendo una caída
de tensión positiva
Como va quedando la ecuación
Suma de la fuentes de tensión =I1
(corriente de la malla 1)*R1+las caídas restantes
Luego me encuentro con la
resistencia R5 la cual es atravesada por dos corrientes la de la malla 1 (I1) y
la de la malla 2 (I2) entonces la caída de tensión en esta resistencia es
positiva debido a la malla 1 y negativa debido a la corriente de la malla 2 ya
que el sentido de esta es contrario al del la corriente de la malla que estoy
planteando
Entonces la ecuación va tomando la SIG forma
Suma de la fuentes de tensión
=I1*R1+I1*R5-I2*R5+las caídas restantes
Por ultimo encuentro la ultima
resistencia antes de completar la malla cuya caída de tensión va a ser positiva
ya que solamente es atravesada por la malla 1
Y al final la ecuación queda
Suma de la fuentes de tensión
=I1*R1+I1*R5-I2*R5+I1*R4
Si agrupamos las I1 obtenemos la
ecuación más ordenada que es
Suma de la fuentes de tensión
=I1*(R1+R5+R4)-I2*R5
Suma de las fuentes de tensión=I1*(10ohm+3ohm+20ohm)-I2*3ohm
Suma de las fuentes de tensión=I1*(33ohm)-I2*3ohm
Malla 2
Partiendo de la fuente 2 la
primer resistencia que me encuentro es R5 cuya caída es positiva debido a I2 y
negativa debido a I1 (al revés que en la malla anterior). Luego tengo la caida
debido a R2 y por ultimo la debido a R3 ambas unicamente afectadas por la
corriente de malla 2, quedando la ecuación de la siguiente forma
Suma de la fuentes de tensión
=I2*R2-I1*R2+I2*R2+I2*R3
Agrupando I2
Suma de la fuentes de tensión =I2*(R5+R2+R3)-I1*R5
Suma de la fuentes de tensión
=I2*(3ohm+5ohm+2ohm)-I1*3ohm
Suma de la fuentes de tensión
=I2*(10ohm)-I1*3ohm
Las Ecuaciones de las mallas
Combinado lo visto en los dos
puntos anteriores
Malla 1
7v = suma de las caidas de
tension en la malla 1
Suma de la fuentes de tensión
=I1*(R1+R5+R4)-I2*R5
Obtengo la ecuación de la malla 1
7V= I1*(33ohm)-I2*3ohm
y
Malla 2
-7v= suma de las caidas de
tension en la malla 2
Suma de la fuentes de tensión
=I2*(R2+R5+R3)-I1*R5
Obtengo la ecuación de la malla 2
-7v= I2*(10ohm)-I1*3ohm
Ecuaciones Finales de mallas
7V= I1*(33ohm)-I2*3ohm
-7v= I2*(10ohm)-I1*3ohm
Paso 4 : Resolución de las ecuaciones de mallas
Bueno hasta acá estábamos bien en
el terreno de la física ,ahora entramos en la parte complicada de la cosa en
tramos en una zona oscura y compleja y sobre todo aburrida el territorio de las
matemáticas esa ciencia oscura que siempre nos rompe la cabeza.
Lo que obtuvimos en el paso
anterior fue un sistema de ecuaciones el cual tiene varias formas de resolución
de las cuales vamos a analizar dos métodos ; el de el determinante y el del
Gauss.
Antes de comenzar a resolver los
sistemas debemos ordenar las ecuaciones es decir que cada incógnita este en una
misma columna
Sistema desordenado Sistema
ordenado
7V= I1*(33ohm)-I2*3ohm 7V=
I1*(33ohm)-I2*3ohm
-7v= I2*(10ohm)-I1*3ohm -7v=- I1*3ohm
+I2*(10ohm)
Fíjense que lo único que hice fue
intercambiar los términos de la segunda ecuación para que quedasen en la misma
columna
Ahora analizaremos la resolución
por el método del determinante.
Utilizando el metodo de las mallas
obtuvimos las sig ecuaciones
Ecuaciones Finales de mallas
7V= I1*(33ohm)-I2*3ohm
-7v= I2*(10ohm)-I1*3ohm
Y ahora estamos de resolver estas
ecuaciones con el metodo del determinante
Primero antes que nada debemos
ordenar las ecuaciones para que las incognitas esten en la misma columa esto se
logra fácilmente intercambiando los terminos de la segunda ecuación
7V=
I1*33ohm-I2*3ohm
-7v=- I1*3ohm+ I2*10ohm
Les recomiendo leer la Entrada anterior Correspondiente a el Metodo del determinante
Ahora planteamos la matriz de
FACTORES y la de cofactores
Fijencen que tomo en cuenta los signos
que acompañan a las corrientes
Ahora calculamos el determinante
de la matriz de factores
Ahora calculamos el determinante
de la matriz de cofactores I1
Ahora calculamos el determinante
de la matriz de cofactores I2
Y por fin calculamos las tan
deseadas corrientes de mallas
Paso 5 : Calculo de las corrientes reales del circuito
Primero analicemos el circuito
con las corrientes planteado en el paso uno
Y ahora las corrientes de mallas planteadas en el paso 2
Y superpongamos ambos esquemas
obteniendo
Ahora la corriente natural o
real (paso 1) de cada rama va a ser igual a la suma de las
corrientes de mallas (paso 2) que van en el mimo sentido que dicha corriente
,menos las corrientes de malla que van en sentido contrario a la corriente
natural.
Osea según el ejemplo
I1(real)=I1 (malla) =0,152 A
Ya que I1 de malla es la unica
corriente que atravieza la rama donde circula I1 real y es positiva porque ambas van enel mismo
sentido
I2(real)=-I2 (malla) =-(-0,654A)=0,654 A
Ya que I2 de malla es la unica
corriente que atravieza la rama donde circula I2 real y es negativa porque
ambas van en sentido contrario
I3(real)= I1 (malla) -I2 (malla) =0,152 A
-(-0,654A)= 0,152 A
+ 0,654 A=0,808 A
Ya que I2 de malla e I 1 de malla
atraviezan la rama donde circula I3
real donde I1 es positiva porque va en
el mismo sentido que la corriente de la rama I3 e I2 es negativa porque va en
sentido contrario a dicha corriente
Ejemplo circuito 2
Ya hemos desarrollado el circuito
mas básico que hay de mallas, ahora debemos ser un poco mas realista y pensemos
en algo que nos pueden tomar en un examen real
Un circuito con tres mallas(mas
adelante veremos porque son tres
Analicemos el circuito según los
pasos ya vistos
Paso 1 : Planteo de las corrientes reales del circuito
Recordemos que el sentido a menos
que no los den por defecto puede ser el que queramos tanto asi como la
denominación de las corrientes yo la planteo asi
Paso 2 : Planteo de las corrientes de malla
Analicemos las mallas del
circuito
Donde digo que tiene tres mallas
porque es el numero minimo de mallas que necesito para que todas las ramas del
circuito queden incluidas dentro de al menos una malla.
Ahora como verán he planteado las
tres mallas en el mismo sentido de giro (horario), mas adelante explicaremos
porque es esto, y como se puede utilizar para salvarnos las papas haciendo las
cosas mas fáciles
Paso 3: Obtension de las ecuaciones de mallas
Malla 1
Recordemos que en el ejemplo
anterior desarrollamos fuentes de tension y caidas de tension en forma
independiente , esto no lo bamos a volver a repetir ya que hace muy engorroso
la explicación y el desarrollo de las ecuaciones
Según el teorema de mallas
Suma de fuentes de tensión en la
malla = suma de las caídas de tensión en la malla
12v + 10 V= I1*10 ohm-I3*10 ohm+5 ohm*
I1-5ohm*I2+2 ohm*I1
Se indica la procedencia de cada
miembro de la ecuación según la grafica

Donde las fuentes de tensión son
positivas porque siguiendo el recorrido de la malla yo salgo por el terminal
positivo. Las caídas de tensión se desarrollan de la siguiente manera . la
primera resistencia que me encuentro es la de 10 ohm la cual produce dos caídas
de tensión , una positiva debido a I1 (ya que va en el mismo sentido que la corriente
de malla que estoy planteando) y una negativa debido a I3 (ya que va sentido contrario que la corriente
de malla que estoy planteando). La segunda
resistencia que me encuentro es la de 5 ohm la cual produce dos caídas
de tensión, una positiva debido a I1 (ya que va en el mismo sentido que la
corriente de malla que estoy planteando) y una negativa debido a I2 (ya que va sentido contrario que la corriente
de malla que estoy planteando). la
tercera resistencia que me encuentro es la de 2 ohm la cual produce una tensión
positiva debido a I1 (ya que va en el mismo sentido que la corriente de malla
que estoy planteando) solo produce una caída de tensión porque es atravesada
por una única corriente de maya, obteniendo asi la siguiente ecuación
12v + 10 V= I1*10 ohm-I3*10 ohm+5 ohm*
I1-5ohm*I2+2 ohm*I1
Agrupando los términos de la
ecuación nos queda que
22V=I1*(10+5+2) ohm- I2 * 5 ohm – I3 * 10 ohm
22V=I1*17 ohm- I2 * 5
ohm – I3 * 10 ohm
Que es la ecuación de la malla 1
MALLA 2
Vamos directamente a plantear la
ecuación
-10 v-5v
=5ohm*I2–5ohm*I1+5ohm*I2–5ohm*I3+2ohm*I2
Se indica la procedencia de cada
miembro de la ecuación según la grafica

Donde las fuentes de tensión son
negativas porque siguiendo el recorrido de la malla yo salgo por el terminal
negativo. Las caídas de tensión se desarrollan de la siguiente manera . la
primera resistencia que me encuentro es la de 5 ohm ohm la cual produce dos
caídas de tensión , una positiva debido a I2 (ya que va en el mismo sentido que
la corriente de malla que estoy planteando) y una negativa debido a I1 (ya que va sentido contrario que la corriente
de malla que estoy planteando). La segunda
resistencia que me encuentro es otra
de 5 ohm esta vez entre la malla
2 y la malla 3 la cual produce dos caídas de tensión, una positiva debido a I2
(ya que va en el mismo sentido que la corriente de malla que estoy planteando)
y una negativa debido a I3 (ya que va
sentido contrario que la corriente de malla que estoy planteando). la tercera resistencia que me encuentro es la
de 2 ohm la cual produce una tensión positiva debido a I2 (ya que va en el
mismo sentido que la corriente de malla que estoy planteando) solo produce una
caída de tensión porque es atravesada por una única corriente de maya,
obteniendo asi la siguiente ecuación
-10 v-5v
=5ohm*I2–5ohm*I1+5ohm*I2–5ohm*I3+2ohm*I2
Agrupando los términos de la
ecuación nos queda que
-10 v-5v =5ohm*I2 +5ohm*I2
+2ohm*I2–5ohm*I1–5ohm*I3
Quedando la ecuación definitiva
de la malla 2
-15 v=12 ohm *I2 – 5 ohm * I1 – 5 ohm * I3
MALLA 3
Proceremos de la misma manera de
la malla anterior
Se indica la procedencia de cada
miembro de la ecuación según la grafica

Donde las fuentes no estan
precentes en esta malla debido a esto la suma de las fuentes de tension es 0V.
Las caídas de tensión se desarrollan de la siguiente manera . la primera
resistencia que me encuentro es la de 3 ohm ohm la cual produce una caída de
tensión , una positiva debido a I3 (ya que va en el mismo sentido que la
corriente de malla que estoy planteando. La segunda resistencia que me encuentro es de 2 ohm la cual produce una caída de tensión, una
positiva debido a I3 (ya que va en el mismo sentido que la corriente de malla
que estoy planteando). la tercera
resistencia que me encuentro es la de 5 ohm la cual produce dos caidas tensión
de tension una positiva debido a I3 (ya
que va en el mismo sentido que la corriente de malla que estoy planteando) y
una negativa debido a I2. la cuarta resistencia que me encuentro es la de 10
ohm la cual produce dos caídas de tensión , una positiva debido a I3 (ya que va
en el mismo sentido que la corriente de malla que estoy planteando) y una
negativa debido a I1 (ya que va sentido
contrario que la corriente de malla que estoy planteando), obteniendo asi la
siguiente ecuación
0v = 3 ohm * I3 + 2 ohm *I3 +5 ohm *I3 – 5 ohm
* I2 + 10 ohm *I3 – 10ohm * I1
Agrupando los términos de la
ecuación nos queda que
0v = 3 ohm * I3 + 2 ohm *I3 +5 ohm *I3+ 10 ohm
*I3 – 5 ohm * I2– 10ohm * I1
Quedando la ecuación definitiva
de la malla 3
0v = 20
ohm *I3 – 5 ohm * I2– 10ohm * I1
4 - Resolución del Sistema de ecuaciones
Juntando las tres ecuaciones obtenidas armamos el sistema de ecuaciones
del circuito
22V =17 ohm*I1- 5 ohm* I2 – 10 ohm * I3
ecuación de la malla 1
-15 v=12 ohm *I2 – 5 ohm * I1 –
5 ohm * I3 ecuación de la malla 2
0v = 20 ohm *I3 – 5 ohm * I2–
10ohm * I1 ecuación de la
malla 3
Ahora procederemos a ordenar las ecuaciones para que cada incognita
quede en la misma columna
22V = 17 ohm*I1 - 5
ohm* I2 – 10 ohm * I3
ecuación de la malla 1
-15 v=– 5 ohm * I1 + 12 ohm
*I2 – 5 ohm
* I3 ecuación de la malla 2
0v = – 10ohm * I1 – 5 ohm * I2 + 20 ohm *I3 ecuación
de la malla 3
Ya obtenido el sistema de
ecuaciones y ordenado sus componentes procederemos a su resolución
Como podemos notar se trata de un
sistema de ecuaciones con tres incógnitas
Como hicimos antes abstraigámonos
de las incógnitas y concentremos nuestra atención en los números recordando que
aquellas incógnitas que no están acompañadas de un numero significan que ese
numero es 1 y que se debe preservar el signo
Calculo del determinante de la
matriz de factores
Se repiten a continuación de la
matriz de factores las primeras dos filas y luego el determinante se calcula
como la suma de los productos de las diagonales completas que bajan(Azules) –
la suma de los productos de las diagonales completas que suben(Rojas), tomando
a entender que diagonal completa es aquella que tiene tres términos.
Calculo del determinante de la
matriz de cofactores I 1
Calculo del determinante de la
matriz de cofactores I2
Calculo del determinante de la
matriz de cofactores I3
Bueno y ahora después de hacer
todo esto que pocos comprenderán para que se hizo calculamos I1, I2 e I3
Pasó 5: Calculo de las corrientes reales del circuito
Primero analicemos el circuito
con las corrientes planteado en el paso uno
Y ahora las corrientes de mallas planteadas en el paso 2
Y superpongamos ambos esquemas
obteniendo
Ahora la corriente natural o
real (paso 1) de cada rama va a ser igual a la suma de las
corrientes de mallas (paso 2) que van en el mimo sentido que dicha corriente,
menos las corrientes de malla que van en sentido contrario a la corriente
natural.
I1 = Im1=1,704 A
Ya que I1 de malla es la única
corriente que atraviesa la rama donde circula I1 real y es positiva porque ambas van en el mismo
sentido
I2 = Im1- Im3=1,704 A – 0,802 A = 0,902 A
Ya que I3 de malla e I 1 de
malla atraviesan la rama donde circula
I2 real donde I1 es positiva porque va
en el mismo sentido que la corriente de la rama I2 e I3 es negativa porque va
en sentido contrario a dicha corriente
I3 =Im1 – Im2=1,704 A – (-0,206) A=1,910 A
Ya que I2 de malla e I 1 de
malla atraviesan la rama donde circula
I3 real donde I1 es positiva porque va
en el mismo sentido que la corriente de la rama I3 e I2 es negativa porque va
en sentido contrario a dicha corriente
I4 = - Im2=- (-0,206)=0,206
Ya que I2 de malla es la única
corriente que atraviesa la rama donde circula I4 real y es NEGATIVA porque ambas van en sentido
CONTRARIO
I5 = - Im2 + Im3=- (-0,206) + 0,802 A=1,008A
Ya que I2 de malla e I 3 de
malla atraviesan la rama donde circula
I5 real donde I3 es positiva porque va
en el mismo sentido que la corriente de la rama I5 e I2 es negativa porque va
en sentido contrario a dicha corriente
I6 = Im3=0,802 A
Ya que I3 de malla es la única
corriente que atraviesa la rama donde circula I6 real y es positiva porque ambas van en el mismo
sentido
NOTA
Porque conviene plantear todas
las corrientes de malla en el mismo sentido simple, la respuesta esta en la
matriz de factores, tomemos la del ejemplo planteado
Si observamos ambos triángulos
son iguales y opuestos, esto se da solo si
las corrientes de mallas tienen el mismo sentido de giro, esto es una
valiosa herramienta para verificar si las ecuaciones están bien planteadas.
Además el término de la diagonal principal (la no marcada) en cada fila es
igual a la suma de todas las resistencias de la malla, esto es otra herramienta
de simplificación.
De esta manera también podemos
enunciar un teorema de mallas simplificado
Teorema de mallas simplificado
La suma de las fuentes de tensión
a lo largo de una trayectoria cerrada con su correspondiente signo es igual a
la suma de todas las resistencias en esa trayectoria por la corriente de la
malla que se están planteando – las resistencias compartidas por otras mallas
por las corrientes con las que se comparten.
Si solo si todas las corrientes de mallas van en el mismo sentido
Ejemplo : utilizaremos el
circuito del ejemplo anterior para demostrar la validez de esto , en el planteo
solo de la malla 1
Malla 1
12v+10v =(10+5+2ohm)*I1-I3*10ohm-I2 * 5 ohm
Como veran es mucho mas rapido
plantear las ecuaciones de esta manera
Ahora vamos con la malla 2
-10v-5v=(5+5+2ohm)*I2-5 ohm * I1- 5 ohm *I3
Ahora la malla 3
0v=(3 + 2 + 5 +10ohm)*I3 –I1*10ohm-I3 * 5ohm
Nota : Metodo del determinante
Es importante saber que no es
necesario usar el metodo del determinante siempre existen calculadoras que
resuelven los sitemas de ecuaciones
automaticamante , ademas para sistemas mas grandes se puede usar el EXEL
Si nos exigen usar el metodo ,
las dos herramintas anteriores son utiles para corrovorar los calculos
obtenidos
Nota : simulado de cicuitos
Con el fin de corrovarar los
calculos cuando estamos practicando es util usar un simuloado tipo El viejo
Electronic work bench aquí les dejo la resolucion del circuito anterior
Ejercicios propuestos
1)
Sol : I=0,481 A
2)
Sol Ir7=0,546 Ir1=0,420 a
3)
Sol I R1=0,824 A I R5=0,035 A
4)
Sol IR7=0,203 IR6=0,003 A IR2
=0,849 A
5)
Sol IR1=0,780 A IR6 =0,210 A
IR9=1,04 A